"Turbo-decoding" of error-correcting codes
using belief networks/graphical models
Project Participants
Introduction
Turbo codes are a new class of error-control coding systems that offer
near optimal performance while requiring only moderate complexity.
It is now known that the widely-used iterative decoding algorithm for turbo-codes
is in fact a special case of a general local message-passing algorithm
for efficiently computing posterior probabilities in acyclic directed graphical
(ADG) models (also known as ``belief networks") .
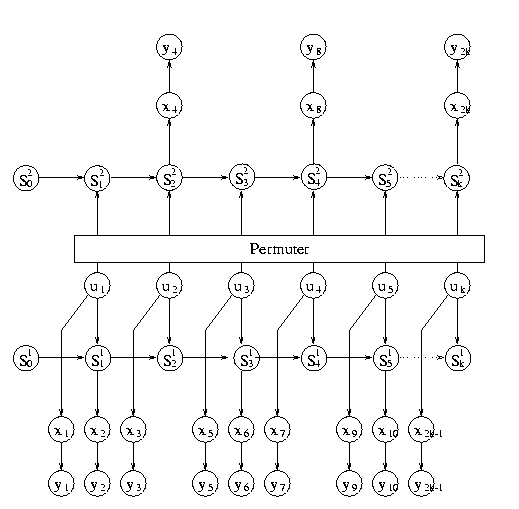
The belief network for rate 1/2 Turbo code is shown below. The information
bits, U1, U2, ..., Uk, are fed into
two convolutional encoders. The codeword X1, X2
,... , X2k, which consists of U1, U2,
..., and the output of the two encoders, is sent across a noisy channel.
The output from the channel is the received
code word Y1, Y2, ... , Y2k.
The Belief Network of Rate 1/2 Turbo code
The message-passing algorithm is valid only in belief networks without
cycles, but the belief network for Turbo code shown above is cyclic.
In this project, we are trying to understand why Turbo code performs so
well in practice.
Results to date
-
Most cycles in the belief network of Turbo code are long cycles.
For example, for the block length of 64000, a randomly chosen node has
a less than 1% chance of being on a cycle of length less than or equal
to 10.
-
The effect of the message from one node is localized in that it cannot
go beyond an effective distance.
Papers
Cooperators and Funding
This is a joint project with Bob
McEliece's group at Caltech, funded by AFOSR.
Related Web Pages of Interest
Information and Computer Science
University of California, Irvine
CA 92697-3425
Last modified: March 29th 1999

