Prediction and modeling of rainfall is an important problem in
atmospheric sciences and agriculture. It is often addressed using
statistical learning methods since global circulation and climate
change models are too coarse and inaccurate to capture properties of
precipitation for a specific location. We consider a problem of
modeling precipitation occurrence for a network of rain stations.
Ideally, the model should capture a number of data properties, e.g.
spatial dependencies between pairs of rain stations, the temporal (e.g.
run-length) distribution of the wet
and dry spell lengths, interannual variability in the
number of rainy days per season. What makes the problem difficult
is the variety of aspects of data to be modeled.
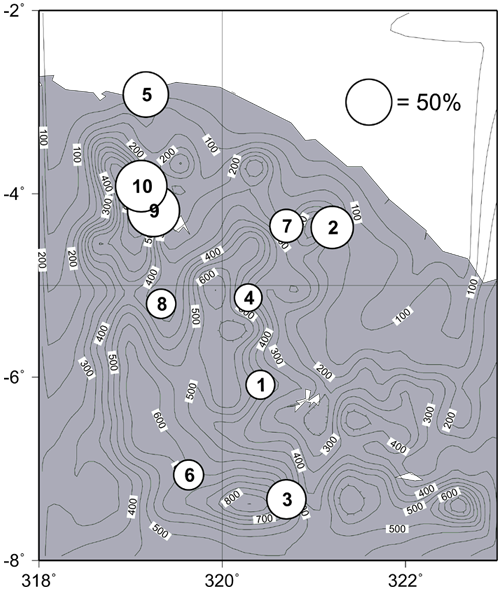
Predicting seasonal rainfall in Northeast region of Brazil is of
great interest to the atmospheric scientists, in particular at
IRI. As one of the goals, they are interested in modeling
rainfall occurrences for February-March-April (FMA) season for the
state of Ceará (Figure 1). The data for the region
consists of
rainfall records for 10 rain-gauge stations for the period beginning at
1975. Once the years with significant number of missing
observations are discarded, we end up with data for 10 rain stations
over 24 years with 90 binary (rain/no rain) observations each.

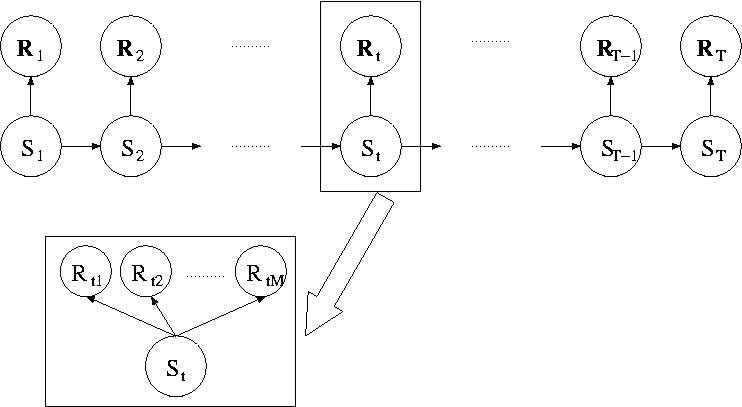
Our approach is to model daily precipitation for the network
conditioned on a small number of "weather" states. The states are
not explicitely known and treated as a random variable. A
sequence of precipitation occurrences is modeled as a hidden Markov
model (HMM) with weather states hidden and having first-order Markov
dependence, and observations for different days independent given the
values of corresponding weather states (Figure 2). Precipitation
occurrences for each station on a given day are further assumed to be
independent conditioned on the value of the weather state.
While this model can capture some global properties of the data, it cannot capture interannual variability due to outside atmospheric factors. For example, using HMMs we cannot predict whether a season from a test data is going be rainier than average or not since there is no mechanism in the model to distinuish unseen sequences. Without a mechanism to use information other than historical precipitation, the model cannot be used for prediction.
Atmoshperic scientists often use general circulation models (GCM) to extrapolate the future physical state of the atmosphere. GCMs can produce with reasonable accuracy values for sea-surface temperatures, sea-surface pressure, wind vectors, precipitation, and other atmospheric variables on a grid of typically 2.5º×2.5º on the daily (or sometimes even finer) time intervals. While these predictions are not accurate enough to predict precipitation for a particular location directly, they can be used as additional input vectors to improve the descriptive power of HMMs as well as to distinguish unseen data. To incorporate atmospheric variables into HMM, we make the transition matrix representing the probability distribution P(St|St-1) dependent on the corresponding value of the atmospheric variable (Figure 3).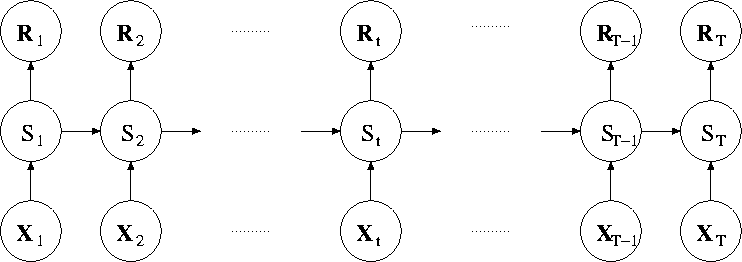
We have used this framework to train models and analyze their
predictive power on the hold-out set for the Northeast Brazil
region. The results are described in detail in the related paper.
This is joint work with Andrew Robertson at the International Research Institute (IRI) for Climate Prediction at Columbia University, and it is supported by the Department of Energy.
Last modified: December 21, 2003