

Next: A Change-point Detection Algorithm
Up: Segmental Semi-Markov Models for
Previous: Introduction
A Viterbi-like Algorithm to Compute the Most Likely
State Sequence (MLSS)
To find the most likely state (i.e., segment label)
sequence
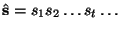 for a data sequence
for a data sequence
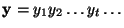 ,
we have the following recursive Viterbi-like algorithm
based on dynamic programming.
At each time
,
we have the following recursive Viterbi-like algorithm
based on dynamic programming.
At each time 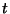 , this algorithm calculates the quantity
, this algorithm calculates the quantity
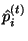 for each for each state
for each for each state 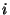 ,
,
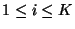 , where
, where
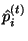 is defined as
is defined as
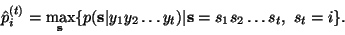 |
(2) |
In other words,
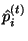 is the likelihood of the most
likely state sequence that ends with state
is the likelihood of the most
likely state sequence that ends with state 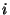 (i.e.,
(i.e., 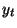 is the last point
of segment
is the last point
of segment 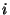 ).
).
The recursive function for calculating
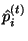 is
is
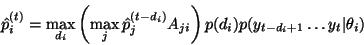 |
(3) |
In the above equation, the outer maximization (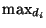 ) is
over all possible values
of the duration
) is
over all possible values
of the duration 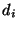 of state
of state 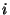 . Recall that
. Recall that 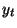 is now fixed to be the last
point of segment
is now fixed to be the last
point of segment 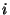 , the last point of the previous segment will be
, the last point of the previous segment will be 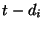 .
For a given
.
For a given 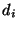 , the inner maximization (
, the inner maximization (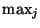 ) is over all possible previous
states
) is over all possible previous
states 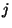 that transitions to state
that transitions to state 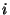 at time
at time 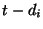 .
The state
.
The state 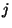 and the time
and the time 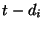 for the maximum value
for the maximum value
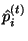 are
recorded in a table denoted as
are
recorded in a table denoted as 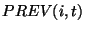 .
.
Obviously, the overall most likely state sequence for the data sequence
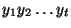 will be the state sequence with the likelihood
will be the state sequence with the likelihood
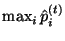 , and can be found by tracing back using the table
, and can be found by tracing back using the table
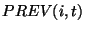 .
.


Next: A Change-point Detection Algorithm
Up: Segmental Semi-Markov Models for
Previous: Introduction
Xianping Ge
2000-05-16
![]() for a data sequence
for a data sequence
![]() ,
we have the following recursive Viterbi-like algorithm
based on dynamic programming.
At each time
,
we have the following recursive Viterbi-like algorithm
based on dynamic programming.
At each time ![]() , this algorithm calculates the quantity
, this algorithm calculates the quantity
![]() for each for each state
for each for each state ![]() ,
,
![]() , where
, where
![]() is defined as
is defined as
![]() is
is
![]() will be the state sequence with the likelihood
will be the state sequence with the likelihood
![]() , and can be found by tracing back using the table
, and can be found by tracing back using the table
![]() .
.