A Change-point Detection Algorithm

The problem of change-point detection can be defined as finding the time of switching from state 1 to state 2 in this model. When inferring the hidden states $\mathbf{s}=s_1 s_2 \ldots s_t \ldots$ from the observed data $\mathbf{y}=y_1 y_2 \ldots y_t \ldots$, also ``missing" are the regression parameters for each segment. This can be addressed by the Expectation-Maximization (EM) algorithm which starts from some initial ``guess" of the regression parameters, and then iterates between the E-step and the M-step. In the E-step, the state probabilities are calculated assuming the regression parameters are fixed. The M-step uses weighted linear regression to estimate the regression parameters for each segment. It can be shown that EM converges to at least a local maximum of the likelihood function in the parameter space.

After EM converges we have point estimates of the regression parameters. For any hypothesized state sequence $\bf {s}$, its decision on the change point $\hat{t}_c^{({\mathbf s})}$ is the time of switching from state 1 to 2. We pool together the decisions of all the state sequences ${\mathbf s}$, weighted by their posterior probabilities $p(\bf {s}\vert\bf {y})$. The estimated change time is the weighted average

$$\hat{t}_c = \sum_{{\mathbf s}} p({\mathbf s}\vert{\mathbf y}) \hat{t}_c^{({\mathbf s})}$$ (4)

The above equation can be evaluated efficiently using $p(s_i \vert {\mathbf y})$.

$$\hat{t}_c = \sum_{{\mathbf s}} p({\mathbf s}\vert{\mathbf y}) \hat{t}_c^{({\mathbf s})}$$

$$= \sum_i \left( i \times \sum_{{\mathbf s}: \hat{t}_c^{({\mathbf s})} = i}p({\mathbf s}\vert{\mathbf y}) \right)$$

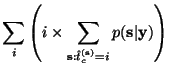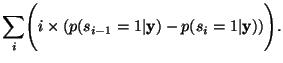$$= \sum_i \Biggl( i \times \left( p(s_{i-1}=1\vert{\mathbf y})-p(s_i=1\vert{\mathbf y}) \right) \Biggr).$$ (5)

We applied the above algorithm to the interferometry sensor data from an etch run on a LAM 9400 plasma etch machine (Fig. 1). The state duration distribution $p(d_i)$ for state $i$ is such that $d_i$ can vary by $\pm 20\%$. The detected change-point is at 232, close to the manually marked 230. The algorithm was also tested on simulated data, and is found to be consistently more accurate than other existing methods (e.g., finding the two segments that minimize the total sum of squared errors.) For more details, see Ge and Smyth (2000b).